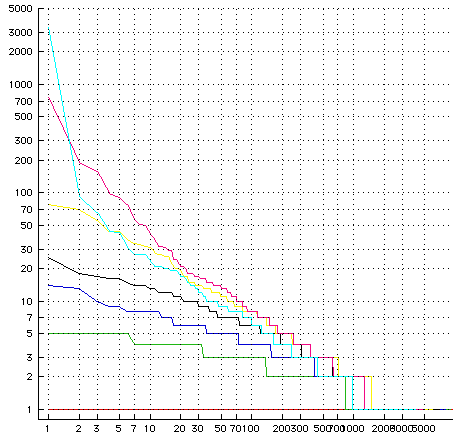
Joi Ito takes a stab at getting his head around what he thinks about the power-law puzzle. Dave Winer comments that he can’t think about the issue because he’s decided he doesn’t like the messenger’s credentials; the messenger in this case being Clay.
The power-law puzzle: We carefully designed a set of networks with the expectation that they would be highly egalitarian, we carefully avoided distribution bottlenecks, we were careful to commoditized the middleman; i.e. end-to-end networks. Much to our surprise when you look at the statistics of the communities that emerge on top of these platforms what you discover is power-law distributions. I.e. distributions of wealth that are frightenly analagous of the worst periods of human history.
For example, Dave Winer thought he was giving everybody their own radio broadcast station when he named his product Radio. Surprisingly the outcome was a lot of radio stations; but only a very small handful captured the vast majority of the listeners. Rather than a peer to peer outcome we got a centralized broadcast outcome.
The same story is true about web servers. We gave everybody the ablity to setup a web server at very low cost. Hundreds of millions took up the opportunity. Today the traffic distributions have settled into a extremely severe power-law curve.
The designers didn’t see this comming. Those same designers need to understand what happen. They might want to consider adding some additional design principles to the next round of systems.
Sticky connections and lousy information are the two things give rise to a power-law distribution.
Lousy information: is the eye of the beholder. Vendors and sellers rarely agree. Newcommers to a network rarely have the right skills to evaluate their choices. Popularity of existing nodes is a poor proxy for real information about what to connect to.
Sticky, sometimes called loyality, is what limits the ablity for a late entrant to displace an early entrant. It’s what gives the wealth time to adapt. Yahoo had to be asleep at the wheel for a very very long time to allow google to even have a chance at displacing them and inspite of that it hasn’t happened. Microsoft could fumble the GUI ball for a decade and still Apple couldn’t displace them.
Joi Ito run at this puzzle is to suggest that the power-law syndrome maybe a useful amplifier for good ideas. That’s true, but only if the system tempers the above two tendencies and if the platform where ideas reside is egalitarian. None of those three is true. Ideas thrive, in a power-law sense, if they spread fast, if they are sticky, and if they can manage to leverage the powerful gatekeepers in the knowledge networks. Those knowledge networks might be the blogsphere, FCC guarded communication networks, the elite acedemic journal networks, or your community’s social network – but you need to get past one of them.
There does appear to be another scenario where good ideas can leverage the power-law to aid their survival. That’s by creating a new network, a new platform. Which remindes me of the old cliche about startups these either go public or get acquired by Microsoft.
That new platforms is another way to work around the powerlaw puzzle in a sense is what Joi is getting at when he writes: “All disruptive technologies and innovations break power law curves by exhibiting exceptional fitness.”
I don’t see that it has anything to do with “exceptional fitness.” Creating a new landscape on which new enterprises rise up isn’t about fitting a niche; it’s about creating a new universe of niches. What grows first on newly exposed land is weeds. They are fit only in the sense that they spread fast. They persist if they manage to keep prevent other more interesting things from displacing them.
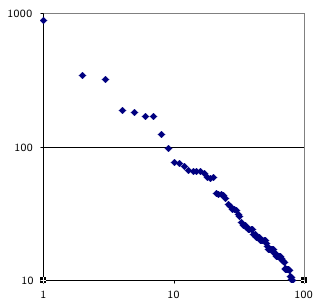 The chart at the right shows has a dot for each of the most popular languages spoken on the planet. It’s plotted on a log-log graph; the vertical axis is millions, the horizontal is rank. The top language is Mandarin, though there are seven other Chinese langages in the top 30. English and Spanish are neck and neck for second place. The data is from here, though originally from here.
The chart at the right shows has a dot for each of the most popular languages spoken on the planet. It’s plotted on a log-log graph; the vertical axis is millions, the horizontal is rank. The top language is Mandarin, though there are seven other Chinese langages in the top 30. English and Spanish are neck and neck for second place. The data is from here, though originally from here.