In my last posting on power-laws (this posting) I illustrated a simple simulation. It grows a network by having each node connect to the network by randomly mimicking the connections made by so far in the network. That model’s important because it gives rise to power-law distributions in the connection wealth of individual nodes. Important because it under cuts the argument that the success of a node is based on it’s quality. It’s not a totally unreasonable model for what happens in markets where the supply chain relationships are very sticky (i.e. we don’t simulate yet any breaking of connections) and the new entrants select their supply chain associations based by modeling existing associations. Such markets aren’t that exceptional in the wake of Moore’s law and his friends.
In this posting I want to look at the advantage of being an early mover into such a market. Older nodes in such a networks tend to be richer, but how much more? The advantage is exponential because the advantages of early entry tend to multiple over time.
Older nodes grow wealth for two reasons. First since the game (the simulation if you prefer) lacks any means for a node to lose wealth the longer you play the greater you chance of getting randomly selected for new connections as the game proceeds. Each connections a node garners becomes an additional generator of luck in future rounds of the game. So connections caught early in the game keep returning value thru-out the game. Secondly the effect is multiplies. Secondly early players are situated in a less competitive game. They have a higher change in each round of winning.
Both of these effects compound so that we can expect that the advantages of getting into the network early to be exponential. An in this graph showing which round a node is born in and how many links it manages to accumulate illustrates that. The horizontal axis is linear. The vertical axis is log base two; thus nodes with only two connections get a score of one.
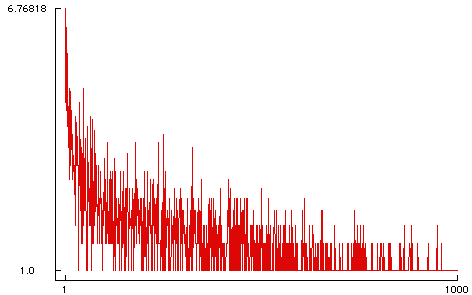
The roughly double expodential distribution of this advantage is clear; but since the fates (i.e. my random number generator) are indeed fickle getting on the bandwagon early doesn’t assure success. One round of the exponential is absorbed in the log vertical scale while the other can be seen if you visualize a fitted line to that noisy data. As you can see, some of the early players gained no long term benefit. I often go to work for those companies.
This graph is only for one run of the simulation but other runs are similar. That graph ought to be a scatter plot, but my graphing tool only does line plots and I’m too lazy to bother to fix it at this point.
All this reminds me of a meeting many years ago where 30 or so very senior technologies sat in a room grilling the senior vice president of a famous desk top software company. The usual problem was a hand. The schedule was slipping, promises had been made, PR as embarrassed, and we had gathered to decide how draconian the cutting would be to get the damn product out.
The question: “Just how important is, time to market?”
The senior vice president allowed as in his experienced it had always appeared to very important, if not more important than all other aspects of the product. Some of us in the room found that to be a less than compelling answer.
He was right. I think we now know why. I’m a believer now!
It’s tended to make less enthusiastic for traditional enthusiasm for process, elegance, care and more enthusiastic for a bias-for-action and a generosity with options that might reveal new networks of oportunity.