Search in a space requires poking around. In fact random search is the canonical strong method. Presuming you have time, can cover the search space, and recognize a solution it can solve any problem. Of course, drunken random walks are well known to result in repeatedly bumping into the same parking meter. So it is with some pleasure that I stumble upon a different kind of random walk. Better yet these walk’s principle feature is that their moves are power law distributed.

Levy walks are observed in nature. Searching animals have only a limited awareness of where food might be found. Outside that awareness they are reduced to random search. But they don’t move randomly in the sense of Browning motion, nor do they randomly select some destination and then move to it. Rather they appear to draw a random number from a highly skewed distribution and then make that move. If you browse the literature on Levy walks you can see that monkeys, humans, and many marine animals all use Levy walks to organize their search. Here’s a picture showing an example of those three kinds of walks.

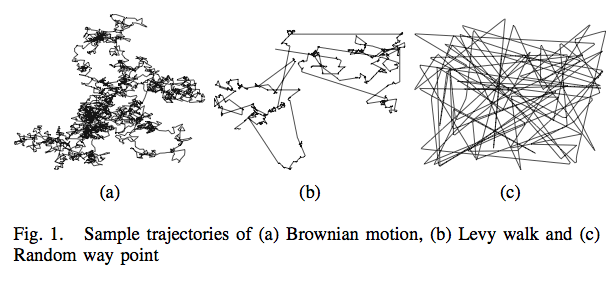
I find this fascinating. As an engineer I’m surprised that I don’t think I’ve ever saw seen a search algorithm using this method. Looking down from above, this means you could observe the trajectory of any object and this simple statistic would tell you if it was alive. Looking out from within, since this is presumably a largely scale free phenomenon it’s quite suggestive about the trajectory of one’s life.